Yes this is a book about trigonometry, well actually it’s more about triangles and how important they are as we don’t get sines, cosines and tangents properly introduced until chapter seven entitled ‘Getting triggy with it’ which tells you all you need to know regarding the wordplay dotted throughout the book. I’ve covered one of Matt Parker’s maths books before, ‘Humble Pi‘ which deals with mathematical errors and like this book I bought it direct from Matt via his website which is full of things that no maths nerd should be without. The extra bonus of being one of the early orders is detailed below but of course the first extra you gain is that books ordered from the site are signed.

The first maths joke you encounter is the price which is £24.85 rather than the expected, and far more normal, £24.99 this is because 2485 is a triangular number of pennies, in this case a triangle with seventy coins on each side. If you’re not familiar with triangular numbers think of the snooker, or pool if you prefer, original setup with fifteen balls in a 5 x 5 x 5 triangle so fifteen is a triangular number with five on each side.

Below you can see the index and immediately you will spot something a little odd because, as he did in ‘Humble Pi’, the page numbering is a somewhat strange. In that book we start at page 314 and count down before hitting an overflow error and leaping up to a huge value, with this book the page numbers are the sine of the angle represented by the page number expressed to six decimal places so they start at zero range up to one and then slowly fall to minus one before rising again to -0.390731 (page 337 in a ‘normal’ book) and yes that does mean that most page numbers occur twice so finding things in the index is a little more tricky than you might expect, more on that later. I knew most of the maths covered in the book although I haven’t used trigonometry seriously for over forty years so a refresher course was interesting. I last had a practical use for trig about ten years ago when I was trying to hang sixteen pictures on a wall in a pleasing display of five on the top and bottom with six evenly spaced across the middle and needed to work out where all the nails should go, preferably before knocking holes in the wall.

The one ‘new’ formula that I hadn’t seen before, even though it is two millennia old was the truly ridiculous Heron’s formula, which gives the area of a triangle, normally expressed as ½ x base x height, but using only the lengths of the three sides a, b, and c without having to calculate the height. Instead you add the three values together, then add any two and subtract the third (for all 3 combinations) then multiply these four values together, extract the square root and divide by four.

Matt actually says “You might need to take a moment to sit down upon hearing that for the first time, I know I did”. Personally I was so confused by what appears to be a series of arbitrary calculations that I sat down and worked out some areas of triangles using ½ x b x h alongside Heron’s formula just to convince myself that it really worked.

And now we come to the index and here Matt has gone a little mad, in ‘Humble Pi’ the index gave the decimal position of the word you are trying to look up, so something given an index value of 23.5 would be half way down page 23. In this book Matt has gone for polar coordinates which is explained at the top of the index. This means that to use it properly you really need a protractor to determine the angle from the bottom left corner of the page. It would also help if he had somehow indicated which of the two possible pages had the page number referred to, for example the first entry ‘A Problem Squared’ is on the second occurrence of page 0.669131. Maybe a suffix r or f for rising or falling as you move along the sine wave of page numbers would work, in this case changing the page number, at least in the index, to 0.669131f

One fun section deals with British road signs that indicate the gradient of an approaching slope in the road. These are normally given as a percentage such as 20% for a 1 in 5 incline however apparently there are still signs which express the value as a ratio and Matt has deliberately left a gap in the text to insert a photo of him pointing at the sign as he fully expects readers who know where one of these is to tell him so he can go there.

Now onto the other reason for buying the book direct from Matt and that is the limited edition alternate covers available. Each of the first 8020 books bought from Maths Gear come with an extra cover with a special design and are all of these are initialled and numbered by Matt, see below.

To explain the extra cover I can do no better than to quote Matt’s website.

As a bonus for anyone who orders direct from me on Maths Gear, I have commissioned three (special, limited) × edition book covers as a collaboration between me and print-artist Paul Catherall. They’re pretty special. You’ll get one free while stocks last.

All books will be signed by me. All book covers will be signed and numbered by me. The first 1,001 orders will get a free “simplex edition” cover, the next 2,024 covers will be “tetrahedron edition” and the remaining 5,995 covers are the “triangle edition”. They will be assigned to orders in that order, so earlier pre-orders get the more-limited cover. Once the covers run out, people will have to be satisfied with just a signed first edition of the book.

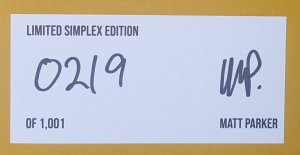
I was early enough to get number 219 of the simplex edition, a simplex is the expression of a triangle in n-dimensions, in two dimensions you get a triangle, in three a tetrahedron, in four dimensions it’s a pentachoron etc. At the point of writing this there are still limited edition covers available but you would have to make do with the triangle design. Sadly 219 is not a triangular number, coming between 210 and 231 however there had to be something special about the value and a bit of digging revealed that 219 is the smallest number that is the sum of four positive cube numbers in two different ways i.e. 1 + 1 + 1 + 216 = 219 and 27 + 64 + 64 + 64 = 219. Thanks to the On-line Encyclopedia of Integer Sequences.

If all of this mathematics has potentially put you off, don’t be. Matt is an excellent presenter of mathematical examples and you really don’t need much grasp of mathematics to follow the majority of the book and you may well learn something, even if it is the crazy formula first written down by Heron of Alexandria over two thousand years ago and which apparently is used today when doing the conversion of file format from a digital image on a phone or digital camera to something that can be printed. So something that ridiculous turns out to have a modern practical application, and yes it surprised Matt as well.

Dear reader, I need you to believe me that I had already written the chapter about triangle laws where I called Heron’s Formula stupid (because it is) when I read the official HP documentation for this technique, and came across the sentence ‘The area of a triangle is given by Heron’s formula’. I honestly just pushed back my chair, stood up and silently left the room, for a walk outside.