
I asked my friend, Catalan booktuber Anna, best known under her nom de plume of Mixa, to choose this weeks read from a random group of titles I provided and she selected Flatland because she had never heard of it and was intrigued by the idea of a mathematical classic combined with social parody. Written in 1884 by an English headmaster who specialised in ‘classics’ i.e. Greek and Latin; this is as an unlikely cornerstone of multi-dimensional non-Euclidean geometry as can really be imagined. I first read it in my teens and although the copy on my shelves is from my mid twenties I probably haven’t read it in over two decades so it is well worth revisiting.
The book is split into two sections, the first describes Flatland and it’s inhabitants whilst the second deals with one of it’s inhabitants A. Square and his perspective of several other lands. Initially Lineland, then what is called Spaceland which is our own set of dimensions and finally Pointland before he finally returns to his own two dimensional world and the prison that we find him in at the start of the narrative.
But let us begin with a description of Flatland because it is with an understanding of this two dimensional land that we will start to see the effects of an extra dimension which is not apparent to the inhabitants. Our narrator A. Square is as you might expect a square and as such is a lawyer, the number of sides that each character has denotes his status in society as follows:
Our Middle Class consists of Equilateral or Equal-Sided Triangles. Our Professional Men and Gentlemen are Squares (to which class I myself belong) and Five-Sided
Figures or Pentagons. Next above these come the Nobility, of whom there are several degrees, beginning at Six-Sided Figures, or Hexagons, and from thence rising in the number of their sides till they receive the honourable title of Polygonal, or many-sided. Finally when the number of the sides becomes so numerous, and the sides themselves so small, that the figure cannot be distinguished from a circle, he is included in the Circular or Priestly order; and this is the highest class of all.It is a Law of Nature with us that a male child shall have one more side than his father, so that each generation shall rise (as a rule) one step in the scale of development and nobility. Thus the son of a Square is a Pentagon; the son of a Pentagon, a Hexagon; and so on.
Below the Equilateral triangles are the ranks of workers and soldiers who are Isosceles and as the size of the smallest angle contained within a figure is an indication of intelligence clearly the more ‘pointed’ such a triangle is the lower the intellect and (bearing in mind this is a Victorian book) the more violent and criminal the individual is assumed to be. Rather than increasing sides with each generation Isosceles triangles gain half a degree to their smallest angle each time until they are finally assessed to be Equilateral and the family can then start to rise through society.
Now it should be noted that as indicated in the quote above this only applies to sons, so what about the females, well they are all just straight lines and this is where Edwin Abbott Abbott (yes the A. in his name really was Abbott as well) hit accusations of misogyny even in the 1880’s. Something he attempted to address in a preface added to the second and revised edition but without much success, one of the more offending sections being below…
Not that it must be for a moment supposed that our Women are destitute of affection. But unfortunately the passion of the moment predominates, in the Frail Sex, over every other consideration. This is, of course, a necessity arising from their unfortunate conformation. For as they have no pretensions to an angle, being inferior in this respect to the very lowest of the Isosceles, they are consequently wholly devoid of brain-power, and have neither reflection, judgement nor forethought, and hardly any memory.
Still enough of the first half of the book, there are lots of details given as to how houses are constructed, how the people recognise each other and various social mores which whilst interesting in the way Abbott has tried to give life to his creation do not really impinge on the main object of the book which is contained in part two. The important section is in the remainder where A Square visits other lands and learns about dimensions other than the North/South, East/West directions he is currently familiar with. The first of these is described as a dream where he perceives Lineland a place of just one dimension with all the inhabitants travelling over a single line with him floating over it so that he can see along the line.
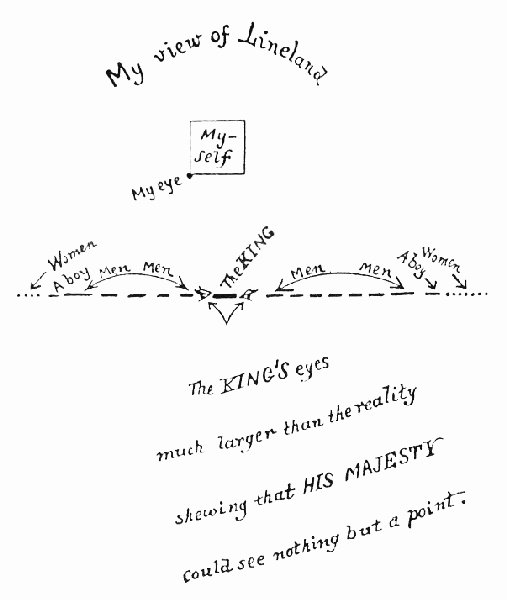
As A. Square interacts with the King of Lineland at first he is simply a disembodied voice coming from nowhere along the line and therefore not perceptible as a figure to his majesty. He therefore lowers himself onto (and through the line) revealing himself as a line as that is all he can be in just one dimension, but a line that can appear and disappear at will. This understanding is vitally important for him to grasp the concept of Spaceland later on in the book when a sphere visits him in his home.

As can be seen from the diagram to A. Square the sphere is merely a circle within Flatland and one that can change size and also appear and disappear just as he could in Lineland but even though he had his dream he still struggles to comprehend what it is that he is seeing until the sphere lifts him off the plane of Flatland and shows him his world from above. Suddenly he can see inside his house and not only that but everyone and everything in it simultaneously. He can even see inside his sons, grandsons and servants and also his wife panicking because he has suddenly vanished.

This is revelatory to him and at this point he grasps a logical progression that had eluded the sphere himself
I. Nay, gracious Teacher, deny me not what I know it is in thy power to perform. Grant me but one glimpse of thine interior, and I am satisfied for ever, remaining henceforth thy docile pupil, thy unemancipable slave, ready to receive all thy teachings and to feed upon the words that fall from thy lips.
Sphere. Well, then, to content and silence you, let me say at once, I would shew you what you wish if I could; but I cannot. Would you have me turn my stomach inside out to oblige you?
I. But my Lord has shewn me the intestines of all my countrymen in the Land of Two Dimensions by taking me with him into the Land of Three. What therefore more easy than now to take his servant on a second journey into the blessed region of the Fourth Dimension, where I shall look down with him once more upon this land of Three Dimensions, and see the inside of every three-dimensioned house, the secrets of the solid earth, the treasures of the mines in Spaceland, and the intestines of every solid living creature, even of the noble and adorable Spheres.
Sphere. But where is this land of Four Dimensions?
I. I know not; but doubtless my Teacher knows.
Sphere. Not I. There is no such land. The very idea of it is utterly inconceivable.
I. Not inconceivable, my Lord, to me, and therefore still less inconceivable to my Master. Nay, I despair not that, even here, in this region of Three Dimensions, your Lordship’s art may make the Fourth Dimension visible to me; just as in the Land of Two Dimensions my Teacher’s skill would fain have opened the eyes of his blind servant to the invisible presence of a Third Dimension, though I saw it not. Let me recall the past. Was I not taught below that when I saw a Line and inferred a Plane, I in reality saw a Third unrecognised Dimension, not the same as brightness, called “height”? And does it not now follow that, in this region, when I see a Plane and infer a Solid, I really see a Fourth unrecognised Dimension, not the same as colour, but existent, though infinitesimal and incapable of measurement? And besides this, there is the Argument from Analogy of Figures.
Sphere. Analogy! Nonsense: what analogy?
I. Your Lordship tempts his servant to see whether he remembers the revelations imparted to him. Trifle not with me, my Lord; I crave, I thirst, for more knowledge. Doubtless we cannot see that other higher Spaceland now, because we have no eye in our stomachs. But, just as there was the realm of Flatland, though the poor puny Lineland Monarch could neither turn to left nor right to discern it, and just as there was close at hand, and touching my frame, the land of Three Dimensions, though I, blind senseless wretch, had no power to touch it, no eye in my interior to discern it, so of a surety there is a Fourth Dimension, which my Lord perceives with the inner eye of thought. And that it must exist my Lord himself has taught me. Or can he have forgotten what he himself imparted to his servant?
In One Dimension, did not a moving Point produce a Line with two terminal points?
In Two Dimensions, did not a moving Line produce a Square with four terminal points?
In Three Dimensions, did not a moving Square produce – did not this eye of mine behold it – that blessed Being, a Cube, with eight terminal points?
And in Four Dimensions shall not a moving Cube – alas, for Analogy, and alas for the Progress of Truth, if it be not so – shall not, I say, the motion of a divine Cube result in a still more divine Organization with sixteen terminal points?
Behold the infallible confirmation of the Series 2, 4, 8, 16; is not this a Geometrical Progression? Is not this – if I might quote my Lord’s own words – “strictly according to Analogy”?
Again, was I not taught by my Lord that as in a Line there are two bounding Points, and in a Square there are four bounding Lines, so in a Cube there must be six bounding Squares? Behold once more the confirming Series, 2, 4, 6; is not this an Arithmetical Progression? And consequently does it not of necessity follow that the more divine offspring of the divine Cube in the Land of Four Dimensions, must
have 8 bounding Cubes; and is not this also, as my Lord has taught me to believe, “strictly according to Analogy”?
Sorry for quoting such a large section but this really is the whole crux of the book as we see that logically there must be a fourth direction that is no more visible to us as up/down was to the square in Flatland and north/south was to the inhabitants of Lineland stuck as they are in their eternal east/west line.
We leave Flatland as we began with A Square in prison for having committed the heresy of declaring of what he calls ‘upward not northward’ and trying to spread these ‘lies’ in Flatland. He is being visited by a priest, as he has been for seven years to try to get him to recant from his madness but instead he determines to write this book.
Flatland has never been out of print since it’s original publication over 130 years ago and it remains one of the great primers in understanding multidimensional geometry so important after the work of Einstein, I heartily recommend it and have thoroughly enjoyed rereading it so thank you Anna.


You’re welcome David! 😉 That was so interesting and funny!
What an original book… Thank you for helping me discover it!
Looking forward to reading your next post,
Mx
LikeLike